TRASLACION Y REFLEXIONDE FIGURAS GEOMÉTRICAS EN EL PLANO CARTESIANO
Traslación y reflexión
TRASLACIÓN:
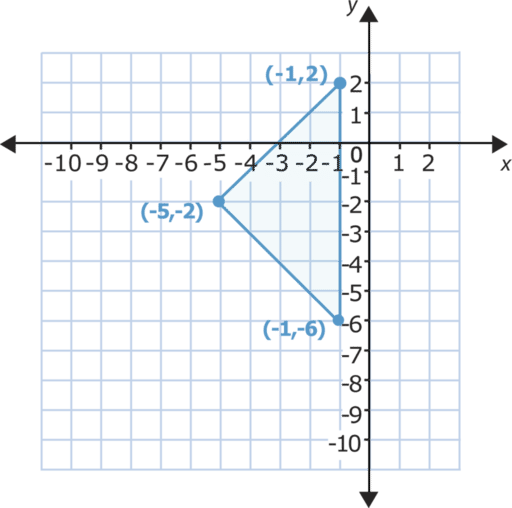
Al realizar una traslación , desplazamos una figura a la derecha, la izquierda, hacia arriba o abajo. Esto implica que las coordenadas de los vértices cambiaran. Observa el siguiente diagrama.
Recuperado de https://www.youtube.com/watch?v=IuWphxWm-_Y&t=6s
Ahora realicemos una traslación de la figura.
Podemos elegir cuantas posiciones y en qué dirección mover el triángulo. Si movemos el triángulo 3 posiciones hacia abajo, todos los vértices del triángulo en el eje y− disminuyen en 3. Esto quiere decir que los pares ordenados de los nuevos vértices cambian. Específicamente, la coordenada y− de cada par disminuye en 3.
Veamos cómo funciona.
Podemos notar cómo cambian las coordenadas de y y− . Compara los puntos superiores. El valor de y− original es 2, luego de moverlo cambia a -1. La coordenada y− disminuye en 3. Ahora compara las puntas izquierdas de cada triángulo. El valor de y− original es -2, luego de moverlo cambia a -5. Nuevamente, la coordenada y− disminuye en 3. En el último punto, el valor original de y− es -6, luego de moverlo cambia a -9. En cada punto, la coordenada y− disminuye en 3 mientras que las coordenadas y− es -6, luego de moverlo cambia a -9. En cada punto, la y− disminuye en 3 mientras que las coordenadas x− se mantienen igual. Esto significa que movimos el triángulo 3 posiciones hacia abajo.
Podemos trasladar las figuras de otras maneras también. Podemos mover las figuras hacia la derecha o la izquierda en el plano cartesiano al cambiar sus valores de x− También podemos mover las figuras en diagonal al cambiar sus valores de x− e y− . cambiarán de igual manera.
Para graficar una traslación, debemos realizar el mismo cambio en cada punto.
REFLEXIÓN:
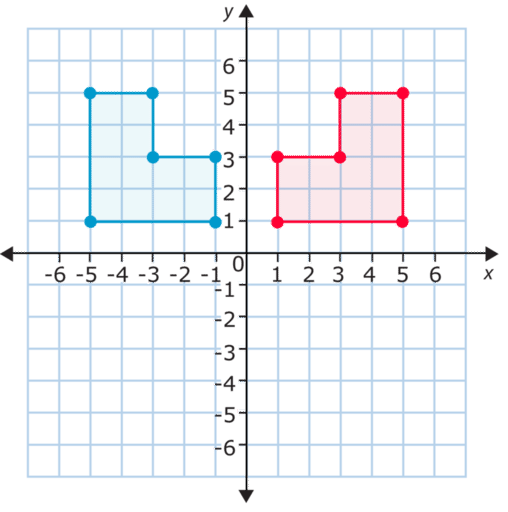
También podemos identificar una reflexión por el cambio en sus coordenadas. Recuerda que en una reflexión, la figura gira para crear una imagen reflejo de sí misma. Observa la reflexión de abajo.
Normalmente las figuras se reflejan sobre el eje x− o el eje y− En este caso, la figura se refleja sobre el eje x− . Si comparamos las figuras del primer ejemplo vértice por vértice, veremos que las coordenadas de x− cambiar pero las de y− se mantienen. Esto se debe a que la reflexión se realizó desde la derecha hacia el eje x− Al reflejar sobre el eje y− las coordenadas de y− cambian y las de x− se mantienen.
Comparemos algunos de los vértices. En la figura de al lado las coordenadas para el vértice superior izquierdo de la figura original son (-5, 5). Al reflejar la figura sobre el eje y− las coordenadas del vértice correspondiente son (-5, -5). ¿Cuáles son las coordenadas del vértice inferior derecho? Las coordenadas originales son (-1, 1) y luego de reflejarla las coordenadas cambian a (-1, -1). Como puedes apreciar solo las coordenadas de x− cambian. De hecho, las coordenadas de y− se convierten en enteros negativos de las originales Esto indica que se trata de una reflexión vertical (arriba/abajo) o una reflexión sobre el eje x− .